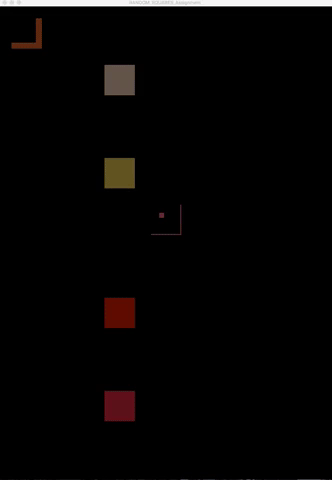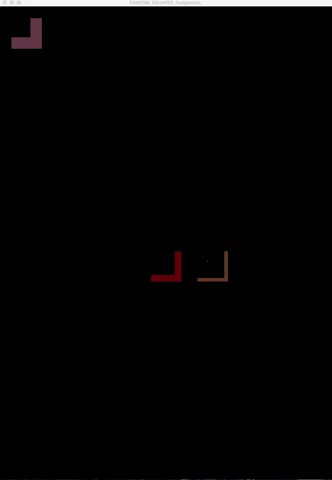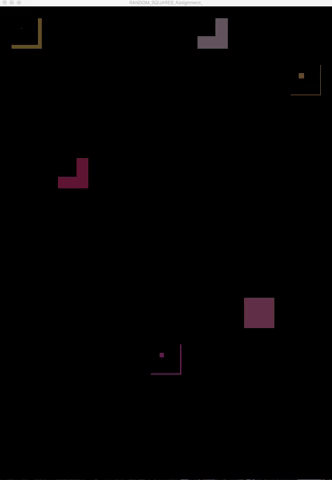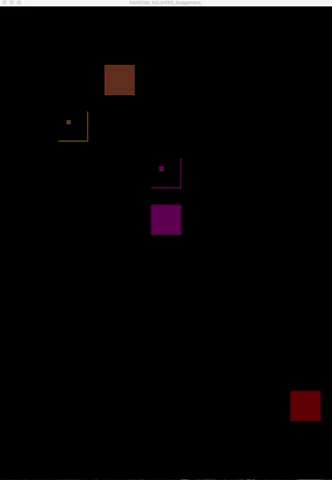Category: [Old] Your Work

The way the make “random” pictures is just incredible. I would really love to discuss more in detail how they created these (3:46 time stamp) pictures. I really love the way they had some sort of variables which can be easily changed. They can choose the shape and the behavior of the shape. Isn’t that incredible? Using these variables that can easily be changed you can create a big load of different pictures/images. All of them are basically created “with a roll of a die” by choosing random variables. More what I like about the video is the “Chance of code” section (22:22 timestamp). There he talks about the history of random pictures using code. An example is the image at 25:27. He says that it is one of the first random pictures generated by a computer using variables. The most interesting part though was how different patterns were drawn in a commander 64. It is really amazing. What amazes me is the way simple characters can create such patterns. Everything we see in our life can have a nice and pretty patterns 🙂

Chance Operations – Casey Reas (Eyeo 2012)

After watching the talk by Casey Reas on chance operations, I was fascinated with the utilization of randomness with sets of control and limitations into a creative and intriguing digital art. From the revolution one line code of repetition and randomness using the Commodore 64 to the current creative platform Processing, the field of using randomness as a core tool has vastly progressed to diverse areas. One of the examples that Reas brought up in his talk was about his use of reproduction of cancer cells data – and how data, with a controlled randomness, can create a unique pattern and open the new era of computer art.

Personally, I found the idea of using simple and individual elements like a dash (-) or a slash (\, /) with controlled randomness  to create a pattern the most interesting – especially relating back to Reas’s co-authored book “10 PRINT CHRS$(205.5+RND(1)); : GOTO 10”. These things may look simple, but the simpleness allow us to look closer and deeper – to use them in unique ways to create something novel. And, Reas’s talk made me to think deeper on the idea of randomness and its application on small components.

The talk, in general, definitely opened me up to numerous ideas and variations that I can apply into previous or existing works, and  raised my excitement in using Processing to make these ideas come true.

Casey Reas, amongst other things, presents works like “Signals” in which he explores how proteins communicate positive and negative signals within a cancer cell.

Randomness. A.I.. Control. Art. Design.

These are all words that exist in the conversation initiated by Raes of and by his work. his talk proceeds to describe the beauty and complexity of randomness in art, and a lot of his own creations, especially in using randomness and “jittering” come to represent much of the organic movements and behaviours we witness in day-to-day life, but cannot quite point to directly.

In describing his works he comes to an interesting notion: that, in creating randomness and behavioural traits, he is not interested in the particular position of an object and any given moment, rather the path of how they organize themselves. Not a moment, but the collection of moments. This idea translates to many tiers of the human experience, whether it be ideological and a way of conceptualizing how paradigms shift, or people and their movement in space.

For me, however, his work represented an important focus in the way we visualize data. How do we collect a point of interest and make it significant for an audience? It is not just Reas using a gimmick to make a pretty object move on a page. Rather the particular movement and the way that he represents that data provided us insight into an aspect of this simulated movement that is unseen to the naked eye.

This is one of my passions in design: to make the unseen, seen. To consider medium, process, and output. To create interaction. Such ideas of visual data and data processing applied in graphics, 2D, and static images. This, in some ways, describes interaction engagement and the exchange of knowledge as things that transcend literal physical interaction.

For the assignment, I recreated “Phase Pattern” by Manfred More with some movement.

//p145 "Phase Pattern" by Manfred Mohr

int w = 400;
int heightDisplacement= 90;
int lineSpacing=6;
float granulation = 0.002;

void setup() {

  size(600, 800);

  //noLoop();
  noFill();
}

void draw() {

  background(20);
  stroke(255);
  strokeWeight(1);
  float prevlengthAdjustment=0;

  for (int y =0; y<height; y=y+lineSpacing) {

    //noise(frequency) , sin a(x+b)

    line(0, y, height, y);
  }
  pushStyle();
  stroke(255, 255, 255);
  fill(0);
  beginShape();
  vertex(1, height);
  for (int x =0; x<width; x=x+8) {
    float frequency2 = frameCount*0.005- granulation*x;
    //-0.002 is granulation. It is to make the noise a little bit smaller. If it wasnt there it would look more random.
    //you multiply by 0.005 to slow down the frame. Otherwise its super fast
    //we multiply by x because it is changing by 1 everytime. If we didnt multiply it, all of the objects will do the same thing.
    float amplitude = 600;
    float adjustedNoise2 = (noise(frequency2));
    float lengthAdjustment2 = adjustedNoise2*amplitude;
    //noise(frequency) , sin a(x+b)




    vertex(x+1, heightDisplacement+lengthAdjustment2);
    //stroke(255, 255, 255);
  }
  vertex(width-8, height);
  endShape();
  popStyle();




  for (int x =0; x<width; x=x+lineSpacing) {
    float frequency = frameCount*0.001+ granulation*x;
    float frequency2 = frameCount*0.005- granulation*x;
    float amplitude = 600;
    float adjustedNoise = (noise(frequency));
    float adjustedNoise2 = (noise(frequency2));
    float lengthAdjustment = adjustedNoise*amplitude;
    float lengthAdjustment2 = adjustedNoise2*amplitude;

    line(x, 0, x, lengthAdjustment);
    line(x+1, 800, x+1, heightDisplacement+lengthAdjustment2);
  }
}

 

Not gonna lie, I was not super excited when I loaded up the link and saw that the video was forty minutes long. But as I started watching it, I totally forgot about the time and just got interested in what Casey Reas was saying. The time passed much faster than I expected.

One of the first things he said was that artists brings order amongst the chaos that nature creates. And I’m not sure I really agree with that. But I also don’t know what artists do in that sense. Because they don’t necessarily bring chaos? Maybe they do bring order? But does nature bring chaos? There are so many ordered things in nature, between all of the patterns you find and the processes that keep it running smoothly, there’s not way it can be classified as “chaos”.

During the last lesson I didn’t quite understand what the purpose of “noise” was. The lecture really helped me understand it, though. The best example was that one where the lines all followed to the same target. If he didn’t add the noise, or “jitter”, then no matter how many lines he added, it would just be a perfect circle around the target. However, with the noise, you could see the individual paths that each line took to reach the target.

One of the distinctions that I was most passionate about that order does not mean unemotional. Order in art does not mean that no thought or emotion or style went into making the piece of art.

Considering that this happened in 2012, I believe that this video shows numerous positive accomplishments that people like Casey Reas have made that are applied in our works today.

To begin with, I want to acknowledge the multi-dimensional aspect of processing. For instance, the work “Signals” done by Casey Reas is an artwork created by technology which portrays the biological procedure of proteins communicating in cancer cells. His artwork already crosses three fields of mastery: art, computer science, and biology. Even on the next example, Reas explains how for years he had been gathering information about certain architecture works before he starts coding. The fact that this individual is able to weave multiple seemingly unrelated works into creating a work that can amaze others is in my opinion very touching and inspiring. His creativity, I believe, is certainly something I can learn of and hopefully apply into my own work.

Michael Noll also contributes greatly to what tools we have today, because I agree with the statement that “the ability to use a rational device to create randomness is amazing”. And not only in military books, or in technical, mathematical programs, it is great to hear from Noll and Reas that randomness in fact can be used to generate creative pieces of work. The element of surprise that people receive when an unexpected result arrives due to randomness is also one of the aesthetics of what we now call a “cool” project.

Overall, Reas helped me re-visualize what kind of projects I would like to do in the future. Now that the lessons I have learned are ingrained within me, I know that IM is one of the few classes where I will be able to really express the creativeness inside me. And to do that, I will definitely refer to the key points of this video: traversing between multiple fields, and using randomness as a tool.

For this assignment, we were asked to recreate one example from a previous Computer and Graphic Art magazine issue.

I picked Random Squares by Bill Kolomyjec, which was published in August 1977: In order to replicate it, I utilized the drawTarget() function, which is helpful when you’re trying to draw multiple separate targets. A few other important functions for making this work are translate(), pushMatrix(), and popMatrix(). I also found this Processing Cheat Sheet to be very handy, it covers most if not all of the basics.

I created a few variations, one that is true to the original, and two where I played around with colors and animation.

Here is the end result of the first variation. However, because the value for the number of squares drawn in each square is randomized, it is not completely identical to the original:

Here is my code:

  boolean playLoop = false; 
      
      void setup(){
        size(930, 1320);
         background(0);
         //frameRate(1); //for loop
         
      }
      void draw(){
      if(playLoop==false){
         for(float x = 0; x<250; x+=25){
         for(float y = 0; y<250; y+=25){
              drawTarget(10, 10, 130, 10); //naming function: first square
              drawsSequence(25); // naming function: translating the shape - repititon
         }
          }
         }
          }
            
            void drawTarget(float x, float y, float size, float scale){
              float space = size/scale; //distance between distinct squares
              float left= space/3; //tightening space between squares on top corner, to mimic visual pattern in the og image
         
              for (int i=0; i<scale; i++){
                rect(x+i*left,y+i*left, size-i*space, size-i*space);
                rectMode(CORNER); // to interpret first two parameters of rectangle as the upper-left corner of the shape
              }
            }
      
       void drawsSequence (int randomNumber){
      float x_=130;
       float y_=130;
        for (int i=0; i<7; i++){
          for (int m=0; m<10; m++){ 
             pushMatrix();
             translate(x_*i, y_*m); // adding new squares
             drawTarget(10,10,130, random(randomNumber)); // randomizing amount
             scale(0.5);
             //fill(112, random(255), 500); 
             //fill(random(255),231, 116);
             popMatrix();
           }
           playLoop = true; //to prevent loop
       }
      }

 

In the second variation, I commented out all the playLoop (true/false) boolean variables , and set the frameRate() to 60 frames per second to animate the shapes. I also set a fill(100, random(100),random(100)) to get a range of randomized dark colors . Here’s how it looked:

And by simply increasing the strokeWeight() to 40, I was able to generate a more abstract form of the variation above. I thought the result was visually appealing. Some of the shapes look a little bit like Arabic characters, and it reminds me of abstract + minimalist calligraphy art:

 

 

 

“The computer is a unique device for the arts since it can function solely as an obedient tool with vast capabilities for controlling complicated processes, but then again, full exploitation of these unique talents for controlled randomness and detailed algorithms could result in an entirely new medium-  a creative artistic medium.” – Micheal Noll

I really enjoyed this presentation by Casey Reas, and I was particularly fascinated by the idea of using code to create generative art where you’re able to control randomness. I especially liked ‘The Tissue Work‘, which was built around ideas from a book by neuroanatomist Valentino Braitenberg. By using software, Reas built a simulation of these conceptual vehicles, and what was interesting was that order began to emerge within their patterns and behaviors over time. To simulate this process, they used order with “a little bit of chance”.

I found the concept of limiting and controlling the amount of randomness in computer art pieces really interesting, and it’s an element that I want to attempt to add to my piece for this week’s assignment, where we are replicating pieces from old issues of a Computer Graphics and Art magazine. Reas mentioned that in one of his projects, they used randomness as a “jumping off point” and I like the idea of utilizing randomness in art as a means of exploring what you can do, but not letting it take up too much of the work’s identity, in a way.

When Reas was talking about chance in art, he provided a few early examples of artists whose works reflect that notion, such as Dada artist Jean Tinguely’s Meta-Matics, a series of machines which automatically produce infinite sequences of drawings:

I really liked this example, especially given that at the time it was made, it was created in response to the then growing commercialization of art and to question the role of the artist amidst the “threat” of industrialization and mass-production. But today, this work has acquired more meaning and it can also be viewed in relation to the idea of exploring technology’s potential as a new medium for art, rather than a substitute.

I picked the computer generated art designed by Hiroshi Kawano for my recreation. Looking at it, I realize that it is black and white only. It also looks random, but there is a certain pattern to it, which reminds me of noise. I thought about how each pixel in the grid is either black or white. I attempted the design by doing a double for loop through the height and width of the screen size. I was able to create noise with the x, y values and multiplying it with a freq of 0.03 ((The image looks tighter if the freq was too high and sparse when the freq is too low)). Depending on whether the noise value is above 0.5 or below, I gave it stroke of either black or white. For each of those pixel in the screen, I made it a point(x, y) so that it would draw something.

From Triangulation:

My Recreation:

If I play with colors and adjust based on grey scale (without (if noiseVal < 0.5)):

The Code:

void setup() {
  size(640, 480);
}

void draw() {
  for (int i = 0; i < width; i++) {
    for (int j = 0; j < height; j++) {
      float freq = 0.03;
      float noiseVal = noise(i * freq, j * freq);
      if (noiseVal < 0.5) {
        stroke(255);
      } else {
        stroke(0);
      }
      strokeWeight(map(noiseVal, 0, 1, 1, 3));
      point(i, j);
    }
  }
}

I then tried to make the noise move since it has a x, y: