Inspiration and Concept
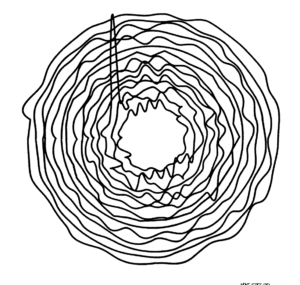
I was looking through some of the works in ProgrammInformation21_PI21 when I came across the sketch below. I immediately thought about the curves I used in last week’s assignment and how noise could be introduced to create this effect of slightly vibrating circles. Essentially, if I drew a circle with curves and then introduced controlled deviations in the vertices’ x and y-coordinates away from the perfect circular path, I would then be able to recreate this piece. In the process of conceptualizing the animation, I also imagined that drawing a curve in each frame would give the illusion of a blossoming flower and add some character and movement to the work. That latter thought effectively lingered in my mind and I found myself experimenting with symmetry, eventually creating an expanding flower animation.
Embedded Sketch
Implementation and Code Highlights
The animation was created by a for loop that creates the curves, nested within another that symmetrically partitions the curve lines to generate petal shapes. I used the Perlin noise() function to allow the curves to wiggle a bit utilizing the iterating variable in the nested for loop and an auxiliary control variable to set the x and y-coordinates in the noise space. This elicited the pattern of organic folds of a flower existing in nature. I referred to the way I created my hair in the last assignment and the examples of using Perlin noise in this article to create the curves. The number of partitions (petals) of the flower is determined by a number that is randomly generated from a finite set of integers. Additionally, the stroke color of each curve is also randomly generated. When set against a black backdrop, the eccentric fluctuations in stroke color produce a glowing effect, which I loved. The animation is replayed when the flower expands to the width of the canvas. Additionally, the animation is repeated with a different number of petals when the mouse is clicked for added interactivity.
// partition the circle based on the variable, petal_partitions_control, to create flower petal effect
for (var j = 0; j < petal_partitions_control; j += 1 / petal_partitions_control) {
beginShape(); // draw curves
for (var i = 0; i < 30; i++) {
// map angle based on current partition iteration
// inner loop implementation inspiration: https://genekogan.com/code/p5js-perlin-noise/
var ang = map(i, 0, 30, j * PI, j * PI + PI / petal_partitions_control);
// generate x and y coordinates using noise for organic shapes
var x = radius * cos(ang) * noise(i * 0.1, perlin_noise_control * 0.05);
var y = radius * sin(ang) * noise(i * 0.1, perlin_noise_control * 0.05);
// draw curve
curveVertex(x, y);
}
endShape();
}
The outer for loop, I would say, is the one I am most proud of as it creates the emergent pattern of flower petals. Admittedly, I do owe Casey Reas and his talk some credit for helping me get inspired to add the symmetry needed to pull this animation together.
Reflection and ideas for future work or improvements
I really enjoyed the process of expanding upon my earlier work and integrating the concepts we discussed in class in the making of this piece. I also loved the process of experimenting with different noise values and stumbling upon the often happy surprises that come with working with randomness and geometry. In the future, I would like to perhaps add more of these flower shapes and give the user some more control in defining the parameters that control the randomness behind the shape (by adding a slider, for example). Additionally, I would love to exploit the same concept to recreate other symmetric shapes – like butterflies – in nature.